Abstract
Counting Y-DNA STR differences is a poor discriminator for members of the same family. Unless a very large number of markers are used, matching cannot be used with a statistically significant degree of accuracy to establish whether someone is more closely related even to second cousins. However there are other methods that may be used to distinguish degrees of relatedness. We present a simple and useful test which involves finding a “segmenting marker” which can establish relative consanguinity with some accuracy, and we give a real-life example of its use to show from which of two 17th Century brothers a man of partly unknown origins descended.
Introduction
The main way in which Y-DNA STRs are currently used in genealogy is to count mismatches in STR values between individuals, which is then used as a broad brush estimator for TMRCA (time to most recent common ancestor). See Walsh (2001)3 and the various online TRMCA estimators which use this method.4
STRs are a good means of establishing whether individuals are unrelated, but they are quite inaccurate in establishing the degree of relatedness for relatives on the paternal line. Unfortunately, the binomial distributions of numbers of mutations are very skewed with wide variances, so that unless a large number of STRs are used, not much statistical discrimination can be expected from counting recent STR mismatches (Walsh 2001 explicitly recognizes this) .
For example a 36/37 marker match has a 95% confidence limit on TMRCA which ranges from 1 generation to 19 generations from the present – a very unsatisfactory result for genealogical purposes. Increasing the number of markers improves the precision of the results, but still not enough to be of much value to traditional genealogists – a 109/111 marker match has a 95% confidence interval of 3 to 22 “transmission events”, or 2 to 11 generations.1 Counting mismatches is indicative but rarely definitive for paper relatives.
Many people coming to genetic genealogy from traditional genealogy expect to be able to use Y-DNA to resolve brickwalls or to find the TMRCA of individuals when paper records are poor. The lack of statistical reliability in counting mutations is particularly disappointing for those hoping to use genetic genealogy as a tool in surname reconstruction.
How inaccurate is counting mismatches?
Consider the common case where we wish to know whether a man (A) is more closely related on the paternal line to relatives (B) or (C). What is the probability that counting the number of mismatches or mutations will get it wrong?
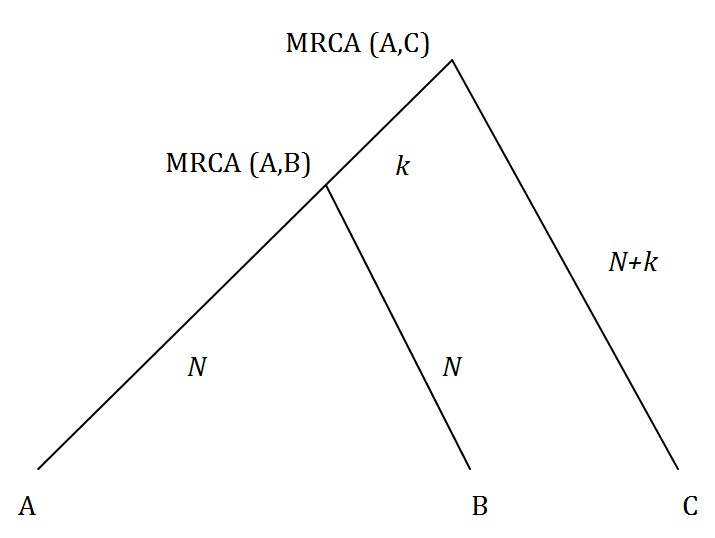
In Figure 1 we show individuals A, B and C in the same family and their most recent common ancestors (MRCA). We are presuming that the number of generations from A, B and C to their common ancestors is the same.
Fig. 1: Individual (A) is closer to relative (B) than (C).
Mutations that occur between A and MRCA (A,B) are irrelevant as they will cause mismatches with both individuals B and C. So we want to know how often the number of mutations in the N generations between B and MRCA (A,B) exceeds or is equal to the number of mutations in the N+2k generations between MRCA (A,B), MRCA (A,C) and C.
The maximum number of STR markers commercially available is 111. How often will mutations in these 111 markers give more mismatches for B than C although B is a closer relative?
Probability of greater number of mismatches of A with B than C. N = generations to MRCA (A, B) k = MRCA (A, C) – N. Calculated as in Appendix.
k
1
2
3
4
5
6
N
2
0.183
0.120
0.079
0.052
0.034
0.022
3
0.224
0.154
0.106
0.072
0.049
0.033
4
0.254
0.179
0.125
0.087
0.060
0.041
6
0.291
0.216
0.159
0.116
0.084
0.060
8
0.315
0.243
0.186
0.140
0.105
0.078
10
0.332
0.263
0.206
0.160
0.123
0.094
Table 1 uses the binomial distribution (see Appendix) to calculate the probability that A and B will appear “further apart” than the more distant relatives A and C, ignoring reversals and parallel mutations. As per the figure, the rows show the number of generations N from A and B to MRCA (A, B) while the columns show the number of further generations k to reach MRCA (A, C). As one might expect, the matching test is more likely to give the right result the closer B is to A in time and the further C is from A and B.
However, for all but a few of the possibilities in the top right of the table (shown as bold), the chance of the test getting it wrong is greater than the 5% confidence limit usually required in statistical inference. With 111 markers the test will distinguish between a second cousin and a seventh cousin (N=3, k=5) with less than 5% error, but nothing closer than that. As well, in this instance B and C can be shown as in the Appendix to have the same number of mismatches with A about 8% of the time, giving an inconclusive result. When k=1, so that we are trying to judge from what brother someone is descended, counting matches is inconclusive or wrong more than half the time even with 111 markers.
The “marker mismatch” test is weakest for N large and k small, which is a common situation. Increasing the number of markers only improves the situation very slowly, and a large number of STR markers are required before the test starts to become statistically significant. If k=2, so that we wish to know from which of two first cousins someone is descended, we would need about 500 markers to obtain a matching test of over 95% significance. Fortunately, there are alternatives.
An alternative – segmenting markers and the “Pairs Rule”
The marker mismatch criterion does not use all the information implicit in a Y-DNA test. For example, marker mismatch does not take into account that mutations happen in sequence along a line of descent.
To make use of the sequential nature of mutations, we can follow a procedure rather similar to what is done in determining the phylogeny of the human genome. Consider what happens when we introduce a third relative D, a referent who is known to be more distant from A than either B or C. The Pairs Rule, which we introduce in this paper, says:
PAIRS RULE: A is closer to B than C if there is a marker which takes the same value for the pair of individuals A and B, and (a different value) for the pair C and D; where D is a more distant “referent” who branches earlier than the other three.
What this says is that the marker “segments the sample” – divides it up into two subgroups with at least two men in each segment. It intuitively makes sense that the men in each segment or subgroup would be more closely related to each other. So because individual D is known to be more distant, C must also be more distant.
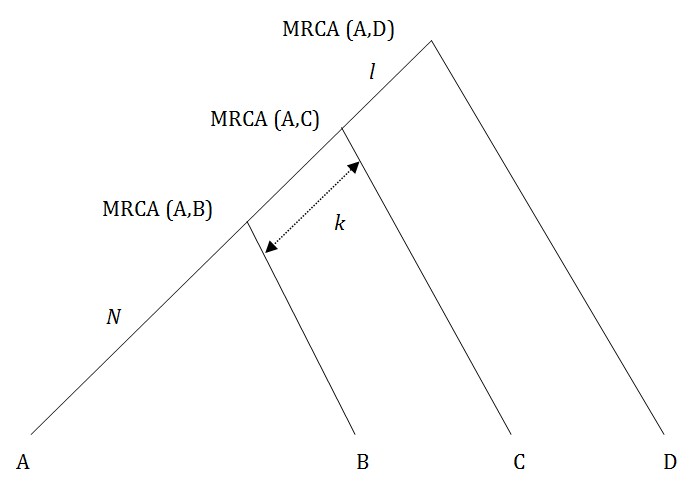
The rationale is shown in Figure 2.
Fig. 2: How a segmenting marker works – mutation in interval k.
What we are looking for is a mutation that takes place in the interval k, before the common ancestor of A and B. Then both A and B will have this mutation and C and D will not. We need the referent D, because if A and B have a different value to C, the change might have taken place on the C line, not in interval k.
If we test enough markers, we will eventually find a segmenting marker mutation that occurs in the interval k. The more generations in k the easier the marker should be to find. If k is small – one might still need to examine hundreds of STR markers – but for more recent relatives, less than counting matches would require for statistical significance. Nevertheless, one might be lucky and find one on a standard test with a small number of markers.
The test gives a false positive (A and C separated from B and D rather than the reverse) when individuals A and C, or B and D, have an identical independent mutation in their post-branching lines. It can also happen if there is a mutation in the interval between MRCA (A,D) and MRCA (A,C) which reverses on the line to B.
The probability of one of these three possibilities occurring may become significant for longer lines The total probability of all three two-mutation combinations is about p2 N (N+k+l) for any individual marker, with N, k and l as in Figure 2 and p the probability of mutation per generation (see Appendix). With N=7 say, this probability is over .0004 per average marker and with 111 markers, the probability of a false positive occurring on one of them may be significant. This probability is of the order of p2, so the test is more convincing if the segmenting marker is slow moving, when a false positive becomes very unlikely.
Example in practice of segmenting markers
To see how the Pairs Rule works in practice, consider the case (real case, names changed) of researcher Alan Coad, who had a genealogical brickwall in the early 1800s but thought he was descended from Henry Coad ~ 1677, whereas I considered Alan was descended from Henry’s brother Edward ~ 1679. We already had DNA from Alan, and from Bob, a descendant of Edward. We found a descendant of Henry, Colin Coad, and Alan convinced him to take a Y-DNA test.
Now conventional matching was not decisive, as well as not significant. Alan matched Bob 67/67 and Colin 66/67, but when we extended out to 111 markers, the matches were 108/111 and 110/111 respectively.
However we could apply the Pairs Rule, because we had Y-DNA from a distant cousin Dennis, who branched from this line at an earlier indeterminate time.
| DYS393 | DYS390 | DYS19 | DYS391 | DYS388 | DYS439 | DYS454 | DYS447 | |
|---|---|---|---|---|---|---|---|---|
| Alan | 13 | 24 | 14 | 11 | 12 | 13 | 11 | 25 |
| Bob | 13 | 24 | 14 | 11 | 12 | 13 | 11 | 25 |
| Colin | 13 | 24 | 14 | 10 | 12 | 13 | 11 | 25 |
| Dennis | 13 | 24 | 14 | 11 | 12 | 14 | 11 | 26 |
| DYS437 | DYS448 | DYS449 | DYS570 | DYS442 | DYS438 | DYS531 | DYS578 | |
| Alan | 14 | 19 | 29 | 17 | 12 | 12 | 11 | 9 |
| Bob | 14 | 19 | 29 | 17 | 12 | 12 | 11 | 9 |
| Colin | 14 | 19 | 29 | 17 | 12 | 12 | 11 | 9 |
| Dennis | 14 | 19 | 30 | 17 | 12 | 12 | 11 | 9 |
| DYS395S1 | DYS590 | DYS537 | DYS425 | DYS594 | DYS436 | DYS490 | DYS534 | |
| Alan | 15-16 | 8 | 10 | 12 | 10 | 12 | 12 | 16 |
| Bob | 15-16 | 8 | 10 | 12 | 10 | 12 | 12 | 16 |
| Colin | 15-16 | 8 | 10 | 12 | 10 | 12 | 12 | 15 |
| Dennis | 15-16 | 8 | 10 | 12 | 10 | 12 | 12 | 15 |
The last marker shown, DYS534, segments the pair of Alan and Bob from the pair of Colin and Dennis. It is the only marker of the whole 111 panel which does so. Therefore, the test says Alan is more closely related to Bob, and is therefore descended from Edward not Henry.
Subsequent conventional research broke Alan’s brickwall, once we knew where to look for answers, and we found that he was indeed descended from Edward Coad ~1679 (how we did this is described in Flood 2013, Chapter 11)2. It turns out that k=2 generations for this example, so we were lucky to find a segmenting marker using only 67 markers.
DYS534 is a fast moving marker– so there is a small possibility that the pairs rule outcome was a false positive. However, it turned out to give the correct result where counting mismatches could not.
The test is simple to administer but requires four relatives, along with some knowledge of the paper relationships in that we need to know the referent (D) is more distant than the other three. It also usually requires a Y-DNA test on 67 markers or more for all four relatives – something that is not always available.
We suspect that most larger surname projects have examples of segmenting markers, and we would like to hear about these from project administrators.
Other uses – non-parental events and pre-surname studies
As well as being useful in large surname projects, the Pairs Rule has applicability to multi-surname phylogeny, in comparing groups of surnames which have DNA matches, to establish the possible order in which lines branched; which ones occurred pre-surname and which might have been due to more recent non-parental events (NPEs) or surname changes – and where there have been several sequential NPEs, in what order they occurred.
In subclade projects too, segmentation might have a role to play. Here, using segmenting markers is actually quite similar to conventional phylogeny where the population is segmented as (+) or (-) on particular SNPs, in which the direction of mutation is determined by matching with an “older” branch. We are using a single STR value in essentially the same way as a SNP, but at a much more recent date.
One must take care however when using segmenting STRs on wider groups than a single family, as independent parallel mutations and reversals become more commonplace in long lines. These can give false phylogenies if we are depending on a single marker to establish descent sequences.
Conclusions
In establishing whether a man is more closely related to or descended from one relative or another, the standard test of counting numbers of STR mismatches is not statistically significant for close relatives unless very large numbers of Y-STRs are used. However, a segmenting marker can give near certainty over shorter lines that someone is related to or descended from one or the other relative. The test requires a fourth more distant relative so that the sequence of mutation can be established.
Segmenting markers should have applications in surname reconstruction in many large surname Y-DNA projects. The technique may also be useful in comparing related men with different surnames. However, identical mutations and reversals on long lines are likely to be a problem as they can produce false results.
Acknowledgements
This article was peer reviewed with 5 commentaries.Appendix 1
MATHEMATICAL CALCULATIONS
This Appendix shows how Table 1 is calculated, and also how the probability of error caused by parallel mutations can be calculated.
a) In table 1 we are seeking to find how often the number of mutations of M=111 markers over N+2k generations is less than the number of mutations over N generations (as per Figure 1). We ignore identical mutations and reversals.
Using Excel formulae, the probability is taken as
Here, we sum over sufficiently many possibilities (taken as 20) the cumulative binomial probability that less than i mutations occur in M markers over N+2k generations, subject to the conditional probability that exactly i mutations occur in M markers over N generations.
To calculate when B and C have the same number of mismatches, we use the similar formula
The average probability of mutation in each of the 111 markers in any generation is taken as p = 0.00251, from Ballantyne et al. (2010)1 .
b) In the diagram of Figure 2, there are three cases when parallel mutations or reversals can result in a false segmenting marker result. For a single marker, each of these three cases involves two separate mutations on two different stretches of the diagram. We have:
Adding (1) to (3) gives p2/2.N. (N+k+l). Further adding (2) gives
p2 N. (N+k+l).
Some of these possibilities can be avoided if we have further information. For example, if we have more lines available down the D path, we might be able to spot any mutations there which are also incurred by B in parallel.
References
- Ballantyne, Kaye N., Goedbloed, Miriam, Fang, Rixun, Schaap, Onno, Lao, Oscar, Wollstein, Andreas, Choi, Ying, van Duijn, Kate, Vermeulen, Mark, Brauer, Silke, Decorte, Ronny, Poetsch, Micaela, von Wurmb-Schwark, Nicole, de Knijff, Peter, Labuda, Damian, Vézina, Hélène, Knoblauch, Hans, Lessig, Rüdiger, Roewer, Lutz, Ploski, Rafal, Dobosz, Tadeusz, Henke, Lotte, Henke, Jürgen, Furtado, Manohar R., Kayser, Manfred. Mutability of Y-Chromosomal Microsatellites: Rates, Characteristics, Molecular Bases, and Forensic Implications. The American Journal of Human Genetics. 2010;87(3):341-353. DOI:10.1016/j.ajhg.2010.08.006.
http://dx.doi.org/10.1016/j.ajhg.2010.08.006 - Flood, J (2013) Unravelling the Code: the Coads and Coodes of Cornwall and Devon. Melbourne: Deluge Publishing.
http://www.lulu.com/shop/joe-flood/unravelling-the-code/paperback/product-21266572.html - Walsh B (2001) Estimating the Time to the Most Recent Common Ancestor for the Y chromosome or Mitochondrial DNA for a Pair of Individuals. Genetics 158, p. 897-912.
http://www.genetics.org/content/158/2/897.long - Clan Donald TMRCA calculator
http://dna-project.clan-donald-usa.org/tmrca.htm